Занати / Столарство / Прорачун гребенасте стеге
Стега чудног имена али невероватно велике примене: гребенаста тј брегаста стега. Ова стега није идеална или квалитетнија замена за остале познатије стеге, али је скоро увек најјевтинија, најпрактичнија и најједноставнија стега.



На претходним примерима види се да је гребенаста стега у ствари нека врста полуге коју "затегнемо" ручном ротацијом око непокретне осовине. На први поглед изгледа једноставно као нека обична полуга која ротира око осовине, али погледајмо сада мало боље ивице те стеге на следећим примерима:
.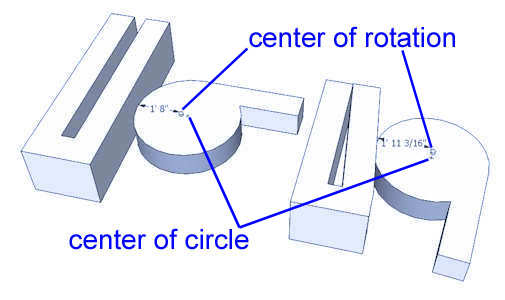

Сада се види да наша стега и није баш тако једноставна како изгледа: њену ивицу чине различите криве линије, што долази до изражаја на последњој слици која приказује низ оваквих полуга спремних за уградњу.
Употреба
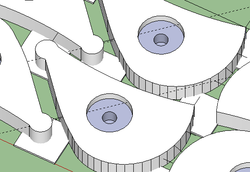
Веровали или не гребенасте полуге имају невероватно велику примену у свим врстама механичких уређаја а посебно у радионичким шаблонима, као што се може видети из следећих сликовитих примера:




Почетни захтеви за пројектовање
Укратко: шта нам је потребно од података пре но што почнемо било какво пројектовање гребенасте полуге? То сам објаснио на следећој слици:
|
О = центар ротације. Положај центра ротације у равни xOy није познат. r = најмање одстојање центра ротације од површине обратка. Ова величина није позната. Плавом бојом у доњем делу скицирао сам дискретан опсег у коме се може затећи горња површина обратка. Обрадак се у ствари може наћи на растојању од центра О у опсегу од r (најмање) до ОЕ (најдаље). |
Ако су ово почетни услови, шта је онда задатак?
Задатак и пројектовање
Погледајмо следећу слику. Задатак је дакле овај: за задати опсег s у коме очекујемо могући полажај обратка, и за задати угао α потребно је одредити величине r1 i r2.
Лако, зар не (наравно сви чекају да чују решење да би на крају рекли: "Па да, знао сам ја то и раније..." Ово је иначе типична српска реакција)?
|
Анализом слике лево добио сам формулу за нападни угао δ: \[\delta [rad] = \alpha - \frac{\pi }{2} - \frac{{\frac{s}{\alpha } \cdot tg(\alpha ) + {r_2}}}{{\frac{s}{\alpha } - {r_2} \cdot tg(\alpha )}}\] Из ове формуле можемо да израчунамо r2: \[{r_2} = \frac{s}{\alpha } * \frac{{\alpha - \pi /2 - \delta - tg\alpha }}{{1 + (\alpha - \pi /2 - \delta )tg\alpha }}\] Овим смо у дакле решили променљиву r2, а тиме добијамо и променљиву r1=r2-s. Знајући r1 добијамо и положај центра ротације изнад највишег могућег положаја површине обратка, чиме је задатак решен. |
На основу последње формуле добијамо минималне димензије металне гребенасте стеге:
| delta= | 3.5° | |
| alfa= | 90° | |
| s | r1 | r2 |
| 1 | 9.4 | 10.4 |
| 2 | 18.8 | 20.8 |
| 3 | 28.1 | 31.1 |
| 4 | 37.5 | 41.5 |
| 5 | 46.9 | 51.9 |
| 6 | 56.3 | 62.3 |
| 7 | 65.7 | 72.7 |
| 8 | 75.1 | 83.1 |
| 9 | 84.4 | 93.4 |
| 10 | 93.8 | 103.8 |
Димензионисање минималне дрвене гребенасте стеге:
| delta= | 10° | |
| alfa= | 90° | stepeni |
| s | r1 | r2 |
| 10 | 25.4 | 35.4 |
| 20 | 50.7 | 70.7 |
| 30 | 76.1 | 106.1 |
| 40 | 101.5 | 141.5 |
| 50 | 126.8 | 176.8 |
| 60 | 152.2 | 212.2 |
| 70 | 177.6 | 247.6 |
| 80 | 202.9 | 282.9 |
| 90 | 228.3 | 318.3 |
| 100 | 253.6 | 353.6 |
Закључак и пример
Како се дакле последње табеле користе у пракси? Претпоставимо да рецимо радите у дрвету и да желите да направите гребенасту стегу која ће покрити опсег нивоа површине обрадка 32мм. На основу друге табеле за s=30mm читате да је r1=76,1mm a r1=106,1mm. Усвајамо рецимо r1=90мм и r1=90+32=122мм.
Остатак је рутински: на папиру цртамо угао 90°, изделимо га на 3-4 дела и повлачимо две кружнице из центра угла са полупречницима 90мм и 122мм. У тачкама пресека кружница са полуправама које деле угао 90° одређујемо пропорционално углу полуправе тачке гребенасте кривине, ове тачке спајамо глатким линијама визуелном интерполацијом и тиме завршавамо цртање кривине гребенасте стеге.
Остаје само да у складу са димензијом расположивог простора одредимо оптималан положај полуге гребенасте стеге. Услов за полугу је да има расположив и за оператера погодан положај и простор од 90° за ротацију.
И наравно, онда одете у своју радионицу и урадите ту гребенасту коначно!

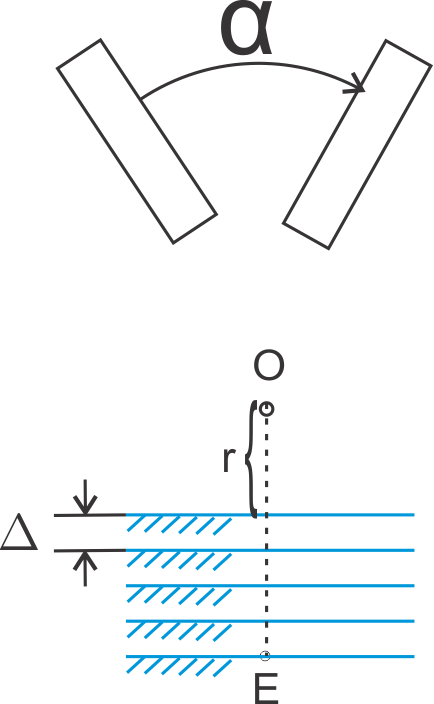 У горњем делу слике приказао сам ручицу која се максимално може окренути за угао
У горњем делу слике приказао сам ручицу која се максимално може окренути за угао 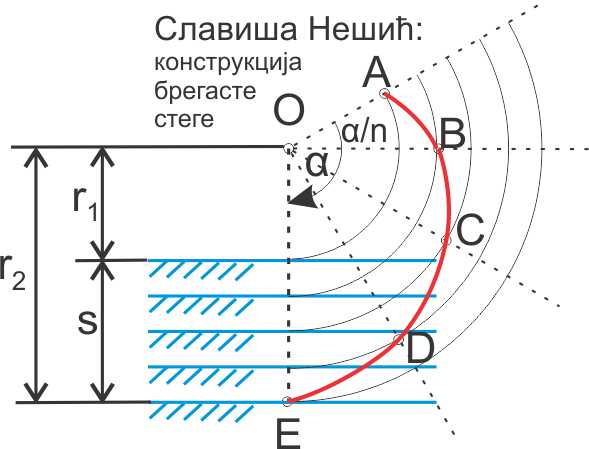 Пре свега треба разумети да кривина полуге (црвена крива линија АBCDE) у тачки додира са обратком има нападни угао
Пре свега треба разумети да кривина полуге (црвена крива линија АBCDE) у тачки додира са обратком има нападни угао